ETF Portfolio Simulator: Methodological and Mathematical Guide

Testing a portfolio before investing helps understand the relationship between risk and return. The Consob reminds that there are no investments that yield a lot with little risk and that diversification is essential to reduce risk. This simulator was created as an educational tool to compare two modes of investment (PIC and PAC) and to analyze how the weights of an ETF portfolio influence returns and volatility.

1. PIC vs PAC and Purpose of the Tool

PIC (lump-sum investment plans) involve one-time contributions to a fund or ETF. PAC (accumulation plans) spread the investment over periodic contributions. Both modes invest in the same instruments, so their risks and returns depend on portfolio composition: a PAC consisting only of stocks will be more volatile and have a higher expected return than a PAC with bonds. Spreading purchases over time reduces the risk of “entering at the wrong time” and encourages discipline (time diversification).

The simulator allows you to reproduce both modes: with an initial amount and monthly deposits you can simulate a PAC, while setting monthly deposits to zero simulates a PIC. The objective is not to provide recommendations but to help you understand how final capital, volatility and drawdown change as you adjust weights.

2. Input Data

The tool uses monthly end-of-month prices for a selection of global and sector ETFs from 2007 to 2025. You can:

• Select the ETFs to include and assign each a weight (the sum of weights must be 1).
• Set an initial amount, a monthly contribution (including zero) and the investment horizon in years.
• Define the number of Monte Carlo simulations to run and, optionally, calculate daily risk metrics.

The input data do not include management fees, transaction costs, taxes or stamp duties. Any dividends are reinvested in the shares (total return data, if available).

3. Mathematical Methodology

3.1 Data Preparation

For each ETF, a series of monthly prices is aligned on the same dates (last price of the month). Returns are the monthly log-returns: r_t = ln(p_t/p_t-1). The portfolio log-return is the weighted average of the ETF log-returns. Accumulating the log-returns yields the performance index (value 1 at the start); the wealth (wealth path) incorporates the initial amount and monthly deposits applied at the beginning of each period before that month's return.

3.2 Backtest Metrics

To evaluate historical performance, classic metrics are calculated:

• CAGR: compound annual growth rate.
• Sharpe ratio: measures the excess return relative to the risk-free rate per unit of total risk (σ). Definition in the glossary of Borsa Italiana.
• Sortino ratio: similar to Sharpe but uses only negative volatility (downside deviation). Definition in the glossary of Borsa Italiana.
• Max Drawdown: maximum loss from peak to trough; see definition in the glossary Morningstar.
• Ulcer Index: the square root of the average of the squares of the percentage losses below the previous peaks (penalizes prolonged losses).
• Time Under Water: average/maximum duration of periods below the previous peak.

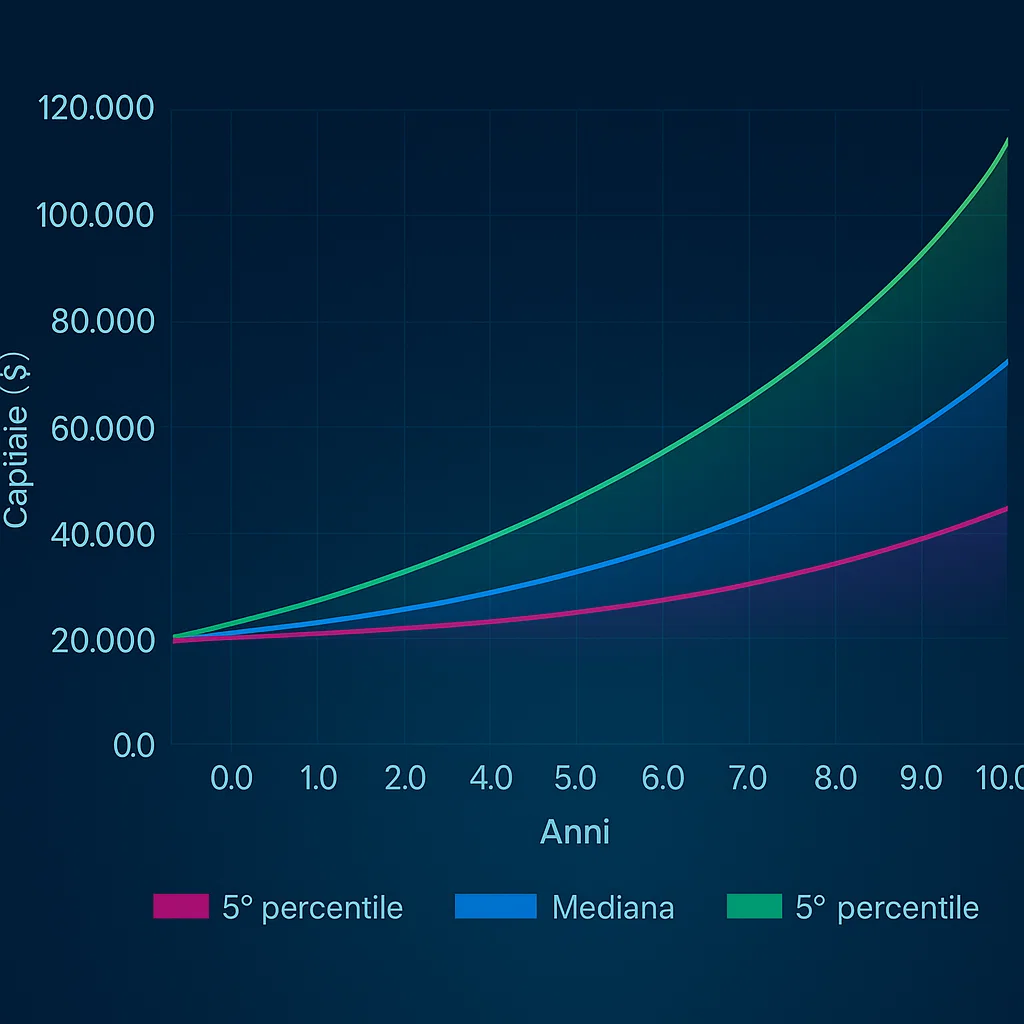
3.3 Monte Carlo Simulations

For each ETF, the mean, standard deviation and correlations of monthly log-returns are estimated. To generate correlated returns, the Cholesky decompositionof the correlation matrix is used and standard normal vectors are sampled; these are scaled (σ) and shifted (μ). Each month: the deposit is added, then the simulated return is applied (multiplying by exp(r)). At the end the percentiles (5th, median, 95th) and metrics (CAGR, Sharpe/Sortino, MaxDD) are calculated on the median path. Key assumptions: normality of returns and stationarity of μ/σ/correlations (simplifying).

4. How to Use the Results

The backtests show how a portfolio with those weights and cash flows would have performed in the past. Monte Carlo simulations generate a range of future outcomes consistent with the historical statistics: the 5th percentile represents an adverse scenario, the 95th a very favourable one. Comparing PIC and PAC you'll notice that the PAC tends to reduce drawdowns and volatility (time diversification) but can give up part of the return if the market rises quickly.

5. Warnings and Limitations

The simulator is for educational purposes. It does not provide financial advice or guarantees of results. The metrics and simulations are based on historical data and statistical assumptions; the future may differ significantly. It is important to consider costs, taxes, slippage and your personal situation: these elements are not modeled by the tool.

6. Sources and References

• Consob – Investment Guide: The Investment Path
• Borsa Italiana – Sharpe ratio and Sortino ratio
• Morningstar – Glossary (Max Drawdown)

Want to try the simulator? Go to the Tools page to enter your ETFs and experiment with PIC and PAC.